iCE is a bitboard engine, which means it sees the board not as a 8x8 array but as a set of 64 bit integers (bitboards) representing the piece locations. So far I only compiled 32 bit code because I was missing a 64 bit OS. This forced the compiler to emulate 64 bit operations by splitting them into 32 bit ones.
I'm now owning a powerful 64 bit monster but I did not compile a 64 bit target yet. iCE is using some inline assembler to speed up some time critical bit operations and this is not portable to 64 bit out of the box. This code must be rewritten and I haven't done this yet.
But as tuning my engine is so CPU intensive I really liked to speed up the engine a bit so I can run the same amount of games in less time. So I rewrote those parts lately.
In order to measure the outcome I produced different 64 bit targets using the Intel and the Microsoft compiler to find the fastest combination. The speed is measured solving a set of 25 positions searched 12 ply deep.
pgo - Profile Guided Optimization is used
popcnt - The popcount processor instruction available on the Nehalem CPUs is used (instead of a software algorithm)
Looks like it is really worth it. The fastest build is about 75% faster than my 32 bit build.
Sunday, April 28, 2013
Sunday, April 21, 2013
Me vs evolution: 0 - 2
The evolved weight set from the last PBIL run was much stronger than my hand selected set, but some of the weights looked suspicious.
The penalty for a double pawn was almost 0, even for a triple pawn very low, a weight related to the pawn shelter was even 0. So I thought I manually correct those values. Just a little bit.
I created a modified set, called ice.tom and let it play another 6000 games against evol-2. But I was not able to improve the set this way. The one coming out from evolution seemed stronger.
Considering the error bars still a tiny chance exists my set is stronger, but I doubt it.
Rank Name Elo + - games score oppo. draws
1 ice.evol-2 89 4 4 18000 55% 51 36%
2 ice.tom 84 7 7 6000 49% 89 43%
3 ice.evol-1 69 5 5 12000 54% 44 33%
4 ice.04 0 5 5 12000 39% 79 28%
For the moment I'm convinced that PBIL is better in tuning than myself.
Saturday, April 13, 2013
Me vs. Evolution: 0 - 1
Now the results are in from some serious genetic evolutions. Here I used knockout tournaments between the individuals within one generation as fitness function.
This is fundamentally different than my former approach were I measured position solving performance
I call them evol-1 and evol-2.
Evol-1 Evol-2
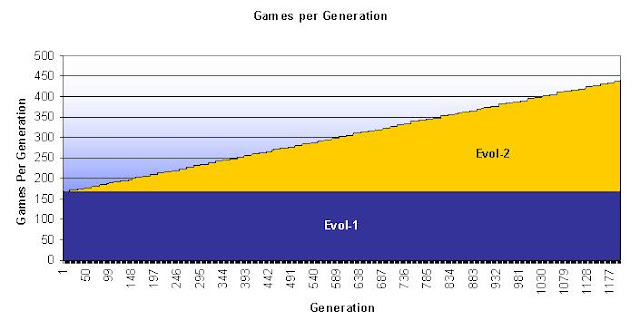
Runtime in hrs 185 363
Generations 1.100 1.200
Total Games 184.800 362.345
EPDs solved* 2.646 2.652
*The number of solved positions out of a test set of 4.109 positions. This number is given to set this GA in relation to the previous test where the number of solved positions was the fitness criteria. Both solutions are better than the un-tuned version that scored only 2.437 points but worse than the version optimized towards solving this set that scored 2.811 points.
So from this data it looks like both versions performed very similar. The fact that version 2 played much more games does not really show up. One explanation could be that the error bar for decisions in both versions is huge, a bit smaller for evol-2 but still huge. So twice as much games doesn't already start to make a big difference.
And finally the real test: A direct round robin comparison between the two and the base version.
And the OSCAR goes to: evol-2
Rank Name Elo + - games score oppo. draws
1 ice.evol-2 89 5 5 12000 58% 35 32%
2 ice.evol-1 69 5 5 12000 54% 44 33%
3 ice.04 0 5 5 12000 39% 79 28%
Looks like all the effort finally paid off, considering also the fact that the base version is also not really a weak engine. It is a bit stronger than the offical iCE 0.3 which is rated 2475 ELO in the CCRL.
Next I maybe tweak manually some of the weights from the final set because some look suspicious. I wonder whether I'm able to score half a point back against the evolution ...
This is fundamentally different than my former approach were I measured position solving performance
- It is computationally much more expensive
- It is not reproducible. If the best individual is determined in a generation chances are very high a different individual would be selected if the calculation would be repeated. This is caused by the high degree of randomness involved when playing small amount of games.
- There is no guarantee that the real best individual is winning a generation tournament. But chances are that at least a good one wins.
I call them evol-1 and evol-2.
Evol-1 Evol-2
Runtime in hrs 185 363
Generations 1.100 1.200
Total Games 184.800 362.345
EPDs solved* 2.646 2.652
*The number of solved positions out of a test set of 4.109 positions. This number is given to set this GA in relation to the previous test where the number of solved positions was the fitness criteria. Both solutions are better than the un-tuned version that scored only 2.437 points but worse than the version optimized towards solving this set that scored 2.811 points.
 |
| Entropy development of evol-1 and evol-2 |
 |
| Comparison of the ability to find correct positions in an EPD file |
And finally the real test: A direct round robin comparison between the two and the base version.
And the OSCAR goes to: evol-2
Rank Name Elo + - games score oppo. draws
1 ice.evol-2 89 5 5 12000 58% 35 32%
2 ice.evol-1 69 5 5 12000 54% 44 33%
3 ice.04 0 5 5 12000 39% 79 28%
Looks like all the effort finally paid off, considering also the fact that the base version is also not really a weak engine. It is a bit stronger than the offical iCE 0.3 which is rated 2475 ELO in the CCRL.
Next I maybe tweak manually some of the weights from the final set because some look suspicious. I wonder whether I'm able to score half a point back against the evolution ...
Saturday, April 6, 2013
How fit is the fitness function
To test that I ran a small tournament between four different versions of iCE.
ice.04 is the base version that uses manual picked weights (reasonable ones but not tuned)
ice.4109 used a training set of 4109 filtered positions
ice.175000 used a training set of 175000 filtered positions
ice.match plays games among the engines within a generation
Here are the results of a 6000 games round robin tournament.
Rank Name Elo + - games score oppo. draws
1 ice.match 52 11 11 3000 60% -17 29%
2 ice.04 14 11 11 3000 53% -5 25%
3 ice.4109 -9 11 11 3000 48% 3 27%
4 ice.175000 -57 11 11 3000 39% 19 24%
Hmm !
Using an EPD solver as fitness function seems not the best choice. That is not a problem of the genetic algorithm itself. It solved what it was told to solve.
The final version of ice.4109 solved 2811 positions out of 4109. The base version of ice.04 only solved 2437 positions. The algorithm definitely found a better solution, unfortunately not for the problem I have.
On the other hand the more complex fitness function that plays games really seems to get the job done, even with a quick and dirty run that was only meant as reference in this case.
So either my approach with EPDs is not good, maybe a 2 ply search per position is not enough (in real games depending on time control iCE searches between 8 and 18 plies in the mid game) or the correlation between single position performance and game play is not strong enough.
It also shows that using more positions doesn't help. This is really surprising.
I still think the EPD approach has potential if it is maybe changed a bit. Things that come into mind here are
- Using a higher search depth to solve each position in the hope to pickup more positional concepts in the then larger tree. But this slows down the algorithm so maybe the population size must be lowered then.
- Modify the fitness function. Currently I award 1 point for a position solved and 0 points otherwise. I could try to award more points for a quiet solution because they are harder to find.
- Splitting the training data into different sets (instead of 1 file with 100k positions make it 50 files with 2k positions) and give each generation a different file. This might prevent the algorithm to converge towards a very specific weight set to solve one file and leads to a more general solution instead, which is stronger in game play.
So more to come ...
Tuesday, April 2, 2013
Inside PBIL for chess eval tuning using EPD data
As a previous post triggered some interest how I used PBIL to auto tune my evaluation I now publish some more details about my approach.
First you have to decide about a fitness function that guides the evolution towards a good solution. The two major approaches I can think of are
The second is closer to the final goal, because at the end you want a strong playing engine and not one that solves a lot of positions, but there seems some correlation between both topics. So an engine that finds the correct move more often is also stronger when playing games. I have yet to find out how strong the correlation is.
When you start thinking about auto tuning with PBIL I suggest you at least start with the 1.st approach (as I did) because of its speed advantages. You can run more evolutions this will help you to get your PBIL framework stable and you can try different settings for the GA to find a suitable set for you (e.g. for Learning Rates, Elitism, Mutation ...).
But before you even start with chess tuning you should solve simpler problems. I used a small matrix problem for that.
A B C
D E F
G H I
where possible values for A - I are 0 - 15. The best solution has the sum of rows and columns all as 24. A working framework should find a perfect solution in no time.
+-----------------------------------------------------------------------+
| Generation: 334 / 500 Population: 100 RunTime: 00:00:01 |
| Worker Threads : 1 Best Fitness: 144 (Age: 131) 0 sec |
+-----------------------------------------------------------------------+
| LR: 0.020/2 NLR: 0.000/1 MP/Drift: 0.000 / 0.050 |
| LR: 0.020/2 NLR: 0.000/1 MP/Drift: 0.000 / 0.050 |
| Elitism: No Entrop: 0.01 |
+-----------------------------------------------------------------------+
| Fitness (-/o/+): 144/144/144 SD: 0 Convergence: 99.990% |
+-----------------------------------------------------------------------+
DNA:
Row1: 10 8 6
Row2: 11 4 9
Row3: 3 12 9
PV Distribution of 36 bits Fitness (mean/max): 144/144
Convergence: 99.99% (0.000%) Entropy: 0.01 (-0.000)
^
| ▄
20 + █
|▄ █
|█ █
|█ █
|█ █
0 +-----+----+----+----+----+----+----+----+----+----+
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Then to the real stuff. When trying to tune an engine with chess positions the selection of "good" positions is very important. Just picking random positions from strong engine games at long time controls is probably not enough. I actually haven't even tried that because I feared that this is a waste of time. The fitness signal might be very weak. A position where the correct move requires a 20 ply search to be found is not very useful. Either no individual in a generation will find it within its search horizon so it does not help to determine the individual fitness or some engines will announce it as best for the wrong reasons.
For similar reasons also positions with tactical solutions (captures, promotions) are less useful because even engines that have the queen value badly wrong will probably go and capture the queen if possible. So almost all engines will solve that, which also does not help to differentiate them.
Therefore I started with positions from games of strong engines but filtered them. I gave them to Stockfish, Houdini and Kommodo and let those engines perform a very shallow search (depth 1or 2). Only if those strong engines were able to find the best move in I considered the position solvable.
The Training Data:
2000 positions, verified with Houdini 1.5a
http://www.fam-petzke.de/downloads/TD-SUB-2000.epd
The EPD file also contains the score that Houdini awarded for that position, I saved it for maybe further use, but have not used it so far.
First you have to decide about a fitness function that guides the evolution towards a good solution. The two major approaches I can think of are
- Let the engine search for a best moves in given positions. Engines finding more correct moves are fitter than others.
- Play games among the engines and their scoring determines the winner in a population
The second is closer to the final goal, because at the end you want a strong playing engine and not one that solves a lot of positions, but there seems some correlation between both topics. So an engine that finds the correct move more often is also stronger when playing games. I have yet to find out how strong the correlation is.
When you start thinking about auto tuning with PBIL I suggest you at least start with the 1.st approach (as I did) because of its speed advantages. You can run more evolutions this will help you to get your PBIL framework stable and you can try different settings for the GA to find a suitable set for you (e.g. for Learning Rates, Elitism, Mutation ...).
But before you even start with chess tuning you should solve simpler problems. I used a small matrix problem for that.
A B C
D E F
G H I
where possible values for A - I are 0 - 15. The best solution has the sum of rows and columns all as 24. A working framework should find a perfect solution in no time.
+-----------------------------------------------------------------------+
| Generation: 334 / 500 Population: 100 RunTime: 00:00:01 |
| Worker Threads : 1 Best Fitness: 144 (Age: 131) 0 sec |
+-----------------------------------------------------------------------+
| LR: 0.020/2 NLR: 0.000/1 MP/Drift: 0.000 / 0.050 |
| LR: 0.020/2 NLR: 0.000/1 MP/Drift: 0.000 / 0.050 |
| Elitism: No Entrop: 0.01 |
+-----------------------------------------------------------------------+
| Fitness (-/o/+): 144/144/144 SD: 0 Convergence: 99.990% |
+-----------------------------------------------------------------------+
DNA:
Row1: 10 8 6
Row2: 11 4 9
Row3: 3 12 9
PV Distribution of 36 bits Fitness (mean/max): 144/144
Convergence: 99.99% (0.000%) Entropy: 0.01 (-0.000)
^
| ▄
20 + █
|▄ █
|█ █
|█ █
|█ █
0 +-----+----+----+----+----+----+----+----+----+----+
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Then to the real stuff. When trying to tune an engine with chess positions the selection of "good" positions is very important. Just picking random positions from strong engine games at long time controls is probably not enough. I actually haven't even tried that because I feared that this is a waste of time. The fitness signal might be very weak. A position where the correct move requires a 20 ply search to be found is not very useful. Either no individual in a generation will find it within its search horizon so it does not help to determine the individual fitness or some engines will announce it as best for the wrong reasons.
For similar reasons also positions with tactical solutions (captures, promotions) are less useful because even engines that have the queen value badly wrong will probably go and capture the queen if possible. So almost all engines will solve that, which also does not help to differentiate them.
Therefore I started with positions from games of strong engines but filtered them. I gave them to Stockfish, Houdini and Kommodo and let those engines perform a very shallow search (depth 1or 2). Only if those strong engines were able to find the best move in I considered the position solvable.
- Stockfish is the best (fastest) engine for that
- Houdini 1.5 is a bit slower probably because of some overhead associated with starting a search
- Kommodo is unstable (once in a while it does not come back with a best move after a "go depth 2" and requires an explicit "stop" command to stop searching)
 |
| Probability Convergence of 507 bits towards 0 or 1 |
 |
| EPDs solved per generation in average and from the best individual (no elitism is used) |
The Training Data:
2000 positions, verified with Houdini 1.5a
http://www.fam-petzke.de/downloads/TD-SUB-2000.epd
The EPD file also contains the score that Houdini awarded for that position, I saved it for maybe further use, but have not used it so far.
Subscribe to:
Comments (Atom)