After the creation of the interesting 3 man table bases I move on to the 4 man stuff. The principle is the same but unfortunately they grow very heavily in size compared to the 3 man tables. At the 1st look they are 64 times bigger because a additional piece with 64 possible squares is included. This means uncompressed takes such a table 30 MB, which is quite a lot if you consider the fact that there are a lot of possible 4 man games and all of them require that space.
So I have to deal with board symmetry properties to contain the space required by the tables. I start with the games without pawns. Here the symmetries are the biggest and I need those tables for the games with the pawns anyway.
I'm starting to think of a conversion method that involves core squares like A1, B1, C1, D1, B2, C2, D2, C3, D3 and D4. Only positions with the white king on a core square are processed. If the white king is not on a core square the board is rotated or flipped and rotated until the white king is on a core square. This should save about 80% of space.
When the conversion is working I will explain it in more detail in a later post.
Sunday, September 26, 2010
Wednesday, September 1, 2010
Creating a KPK endgame table base
After creating the KQK and KRK table bases I go to the more difficult stuff, which is a table base that involves pawns. I create a KPK (King and Pawn vs King) table base. There are 2 reasons that make this more difficult
First I initialize the table with the knowledge from the KQK table base. So on every promotion square I put a queen and score all possible positions with the score of that position from the KQK table base.
Here I encountered the first trap. Usually it is best to promote to a queen but not always.
Promoting the pawn to a queen will draw. The only winning move is under promoting the pawn to a rook. So when initializing the table make sure you consider rook promotions too when they score better than queen promotions.
After initializing the table I very much follow the method of generating positions further away from the known ones until all linked positions are generated and the table is no longer improved. The remaining unlinked unknown ones are draws. I ended up with a good table where the longest distance to mate was a "Mate in 28". But after verifying the content I found out that some positions were incorrectly scored.
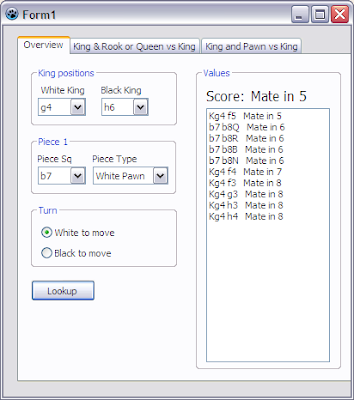
This position was scored "Mate in 6". In fact it is a "Mate in 5". The reason is that I traced positions back from positions were the pawn was promoted and if in the position above the pawn moves to b8 and promotes to a queen it will in fact require 6 moves to mate (incl. the pawn move). However the move Kf5 will already "Mate in 5". But when this position was scored the position with the king on f5 was yet unknown and therefore the "Mate in 6" score was awarded to that position.
I tried several table generation methods that work around that issue (like only initializing with Mated in 0 scores) but all failed. The generated tables were worse than the one I already had. I finally accepted that the first pass will generated positions with paths to mates that are not necessarily the shortest ones.
I then tried a second pass on the filled table were I adjust the scores. I start with the Mated in 1 positions and verify them whether they are truly Mated in 1, I then verify the Mate in 2 positions whether shorter Mates are possible and so on until the "Mate in 28" positions are verified. The algorithm did quite some adjustments, much more than I expected, but the adjusted table now seems to be correct (My table access code does not distinguish between the promotions, it scores all promotions with the best score from a promotion, but this is just cosmetics, the only important thing is the correct score of each position).
- There is no mate position with a King and Pawn vs King. So you cannot just use the plain creation method from KQK here. You must promote the pawn to a queen or a rook before you can mate the king.
- White pawns and black pawns move in different directions. In a KQK endgame it makes no difference when you have a queen on b7 and it is the turn from the one with the queen, whether this is a black or a white queen. The distance to mate will be the same for both sides. In a KPK endgame a white pawn on b7 is very much different from a black pawn on b7.
First I initialize the table with the knowledge from the KQK table base. So on every promotion square I put a queen and score all possible positions with the score of that position from the KQK table base.
Here I encountered the first trap. Usually it is best to promote to a queen but not always.
Promoting the pawn to a queen will draw. The only winning move is under promoting the pawn to a rook. So when initializing the table make sure you consider rook promotions too when they score better than queen promotions.
After initializing the table I very much follow the method of generating positions further away from the known ones until all linked positions are generated and the table is no longer improved. The remaining unlinked unknown ones are draws. I ended up with a good table where the longest distance to mate was a "Mate in 28". But after verifying the content I found out that some positions were incorrectly scored.
This position was scored "Mate in 6". In fact it is a "Mate in 5". The reason is that I traced positions back from positions were the pawn was promoted and if in the position above the pawn moves to b8 and promotes to a queen it will in fact require 6 moves to mate (incl. the pawn move). However the move Kf5 will already "Mate in 5". But when this position was scored the position with the king on f5 was yet unknown and therefore the "Mate in 6" score was awarded to that position.
I tried several table generation methods that work around that issue (like only initializing with Mated in 0 scores) but all failed. The generated tables were worse than the one I already had. I finally accepted that the first pass will generated positions with paths to mates that are not necessarily the shortest ones.
I then tried a second pass on the filled table were I adjust the scores. I start with the Mated in 1 positions and verify them whether they are truly Mated in 1, I then verify the Mate in 2 positions whether shorter Mates are possible and so on until the "Mate in 28" positions are verified. The algorithm did quite some adjustments, much more than I expected, but the adjusted table now seems to be correct (My table access code does not distinguish between the promotions, it scores all promotions with the best score from a promotion, but this is just cosmetics, the only important thing is the correct score of each position).
Subscribe to:
Posts (Atom)