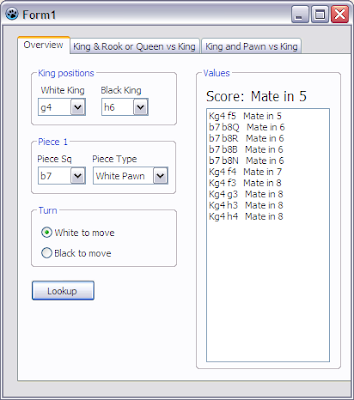
In order to track the progress on the engine and also to compare different features between my mACE and the iCE engine I felt to need to be able to run test positions against the engines.
So far I test single mid game positions before and after some changes, Usually the change was so significant that testing a single position showed the outcome very clearly (adding 0 move or LMR). For a better estiamtion of change impact I need a more comprehensive test setup.
There are test suites available in the internet containing EPD position lines. A EPD line is a basically a position in FEN notation and a best move command, that gives the best move in that position. Running such a test suite against an engine will be much better than running simple positions.
There are available programs on the net that do EPD stress tests with engines, but I rather programmed my own test arena, so I can tweak it a bit better to the results I want to have.
The arena is now done and part of the GUI.
Tuesday, December 28, 2010
Sunday, December 19, 2010
Detecting Three-fold repetition
While designing the new engine I thought about a way to efficiently detect two-fold and three-fold repetitions. My PASCAL mACE engine stores the hash keys of all positions that happened on the board and when a new position is added it looks through the last ones (up to the last pawn move or capture) whether this key shows up in the history. This is very safe, not too bad, but it involves a loop every time a move is made.
Maybe there are better ways of doing that, I thought about a special hash table that only stores a counter for every position that is incremented when the move to that positions is made and decremented when the moves is unmade (in search this happens very often). This would be pretty fast, but what about hash table collisions. Two different positions on the board map to the same hash slot. Are the likely, do I have to care about them.
So question is, in a game of maybe 200 moves, how likely is it that in a table of lets say 32.768 slots 2 different positions map to the same slot. This would confuse the repetition counter and lead to incorrect results.
When you consider the numbers (200 moves, 32768 slots) you might think that is is very unlikely that two positions collide, but in fact it is rather likely. The probability is about 46%. So it that setup every other game you would end up with incorrect repetition detection, which is not acceptable.
How does the probability change when I increase the the hash size. I created a little spreadsheet, that did this for me. The probability P for a collision is P = 1 - (y/(y-x))^(y-x) * e^-x
So it shows that even with large hash sizes a significant probability remains that a collision occurs, I have to find a smart way of handling them.
Maybe there are better ways of doing that, I thought about a special hash table that only stores a counter for every position that is incremented when the move to that positions is made and decremented when the moves is unmade (in search this happens very often). This would be pretty fast, but what about hash table collisions. Two different positions on the board map to the same hash slot. Are the likely, do I have to care about them.
So question is, in a game of maybe 200 moves, how likely is it that in a table of lets say 32.768 slots 2 different positions map to the same slot. This would confuse the repetition counter and lead to incorrect results.
When you consider the numbers (200 moves, 32768 slots) you might think that is is very unlikely that two positions collide, but in fact it is rather likely. The probability is about 46%. So it that setup every other game you would end up with incorrect repetition detection, which is not acceptable.
How does the probability change when I increase the the hash size. I created a little spreadsheet, that did this for me. The probability P for a collision is P = 1 - (y/(y-x))^(y-x) * e^-x
So it shows that even with large hash sizes a significant probability remains that a collision occurs, I have to find a smart way of handling them.
Thursday, December 16, 2010
The prototype of a C++ engine is done
The first version of a new C++ based chess engine that knows the rules and can play random legal moves is done. There is still a awful lot of programming work left as basically the only real thing already working is the move generator, but as far as I can tell it looks promising.
It generates moves faster than my Free Pascal based engine. But probably it is rather from a different implementation of things than by the change of programming language.
And the Mates looked like this
It generates moves faster than my Free Pascal based engine. But probably it is rather from a different implementation of things than by the change of programming language.
- I avoided to use threads, in C++ on Windows you can use PeekNamedPipe to mange unblocking IO.
- I implemented magic bitboards instead of rotated bitboards (It was far easier to implement, the board transformations for rotated bitboards were really mind bending)
- I used int as TMove representation
And the Mates looked like this
Monday, December 13, 2010
Prototyping a new chess engine
After careful consideration I decided to start a parallel engine project for a new chess engine written in C++. This means that the work on my free pascal engine is frozen for the moment as I cannot develop two engines in parallel. Especially the mental switching between Pascal and C++ syntax is quite difficult.
Such small bugs like
Pascal: if sideToMove = WHITE then perform something;
C++ : if (sideToMove = WHITE) perform something; // this is a bug, must be if (sideToMove == WHITE) ...
make the programming difficult. My older formed Borland compiler warned when it encountered such statements (was very helpful). Visual C++ warns sometimes when it is suspicious about the involved types but not always.
So at the moment I put my efforts on a chess engine skeleton in C++. So especially the board class, where the moves are generated and executed will require some time. I wonder what the new perft values will be compared to my Pascal based mACE engine.
I hope that using magic bit boards and using plain int as move type will pay off somehow too.
Such small bugs like
Pascal: if sideToMove = WHITE then perform something;
C++ : if (sideToMove = WHITE) perform something; // this is a bug, must be if (sideToMove == WHITE) ...
make the programming difficult. My older formed Borland compiler warned when it encountered such statements (was very helpful). Visual C++ warns sometimes when it is suspicious about the involved types but not always.
So at the moment I put my efforts on a chess engine skeleton in C++. So especially the board class, where the moves are generated and executed will require some time. I wonder what the new perft values will be compared to my Pascal based mACE engine.
I hope that using magic bit boards and using plain int as move type will pay off somehow too.
Monday, December 6, 2010
Chess Engine Design Considerations
My MACE engine is now functional, it does not play very strong yet, so if competing against other engines it loses most of the time. I think I can improved it by tuning the evaluation function, but this will not fix one of the fundamental problems of the engine.
It is too slow !
Slow relates here to the raw speed "nodes per second".
Using intelligent pruning methods like NULL move or LMR one can reduce the number of nodes the engine considers but there are limits to that. In one point in time the engine is faced with a number of nodes it just has to evaluate. And if it is slow in doing that it will not reach the depths necessary to compete with other engines. It also makes the transposition table less useful as it does contain lesser nodes compared with a fast engine.
I have considered several options to increase the speed
This requires some major changes to the engine and option 3 is probably not possible with Free Pascal.
I think instead of rewriting large parts of the code about starting a parallel engine project using C++ as language. I've not used C++ for quite some time so I'm probably a lot slower programming at first but it helps me refreshing my skills, which is quite necessary I think.
It is too slow !
Slow relates here to the raw speed "nodes per second".
Using intelligent pruning methods like NULL move or LMR one can reduce the number of nodes the engine considers but there are limits to that. In one point in time the engine is faced with a number of nodes it just has to evaluate. And if it is slow in doing that it will not reach the depths necessary to compete with other engines. It also makes the transposition table less useful as it does contain lesser nodes compared with a fast engine.
I have considered several options to increase the speed
- Dropping the TMove class and using plain integers as move (saving the construction and destruction)
- Using magic bitboards instead of rotated bitboards (should increase move generation and execution)
- Dropping the IO thread that is listening on stdin for new commands, making the engine single threaded and saving the shared memory handling overhead
This requires some major changes to the engine and option 3 is probably not possible with Free Pascal.
I think instead of rewriting large parts of the code about starting a parallel engine project using C++ as language. I've not used C++ for quite some time so I'm probably a lot slower programming at first but it helps me refreshing my skills, which is quite necessary I think.
Monday, November 22, 2010
The horizon effect
After some weeks I spend time on the endgame table bases I went back to the engine search algorithms. I let it play some games against other engines and as usual it lost most of them. It is still pretty weak. But from watching the games I try to spot the areas were it is especially weak.
In one game it encountered the following position playing with White
Its time control allowed it a search 8 plys deep. It came up with the move Bb2 (and expecting black to play Re8 as response). Of course black did play e4-e5, forking the knight and the bishop with its pawn and White lost the game.
I tried to find out why White did make such an easy mistake and did not see this obvious threat. It is quite difficult to debug the recursive search algorithm, but at the end I think it lost because it pushed the threat e4-e5 beyond its search horizon of 8 ply.
I check what it calculated for the sequence 8. Bb2 e5. It showed 9. Nxd6 Qxd6 10. Be5 Qd7 11. Bxf6 as principle variation leading to the position
So white was able to push the loss of the bishop or knight by the pawn fork beyond its horizon by playing a series of equal captures and played a weak move because of that.
How do I prevent this from happening again. I came up with 2 possible solutions. The first is to try to handle such threats like a pawn fork in the evaluation, but this might be difficult, the forking pawn must be protected if a bishop mover is forked in order for the fork to work. One of the forked pieces might move away and building up a threat that must be handled (e.g checking the opponents king), then the fork is also not a real threat because both pieces can move away.
The second is the implementation of a recapture extension, whenever a piece of the board is captured after it captured a piece of the same value (a recapture) search is extended one ply. This makes it more difficult for the engine to push something beyond its horizon with equal captures but it also slows down the search in general.
Probably I go for the 2nd option, I will post my progress in a later post then.
In one game it encountered the following position playing with White
rnbq1rk1/pp3ppp/3b1n2/1Nppp3/8/1P1BPN2/P1PP1PPP/R1BQ1RK1 w - - 0 8
Its time control allowed it a search 8 plys deep. It came up with the move Bb2 (and expecting black to play Re8 as response). Of course black did play e4-e5, forking the knight and the bishop with its pawn and White lost the game.
I tried to find out why White did make such an easy mistake and did not see this obvious threat. It is quite difficult to debug the recursive search algorithm, but at the end I think it lost because it pushed the threat e4-e5 beyond its search horizon of 8 ply.
I check what it calculated for the sequence 8. Bb2 e5. It showed 9. Nxd6 Qxd6 10. Be5 Qd7 11. Bxf6 as principle variation leading to the position
rnb2rk1/pp2qppp/5B2/2pp4/4p3/1P1BPN2/P1PP1PPP/R2Q1RK1 b - - 0 12
This position was its search horizon and got evaluated. Quiescence search did not help because after black capturing the bishop white cannot make a winning capture and QS terminates.So white was able to push the loss of the bishop or knight by the pawn fork beyond its horizon by playing a series of equal captures and played a weak move because of that.
How do I prevent this from happening again. I came up with 2 possible solutions. The first is to try to handle such threats like a pawn fork in the evaluation, but this might be difficult, the forking pawn must be protected if a bishop mover is forked in order for the fork to work. One of the forked pieces might move away and building up a threat that must be handled (e.g checking the opponents king), then the fork is also not a real threat because both pieces can move away.
The second is the implementation of a recapture extension, whenever a piece of the board is captured after it captured a piece of the same value (a recapture) search is extended one ply. This makes it more difficult for the engine to push something beyond its horizon with equal captures but it also slows down the search in general.
Probably I go for the 2nd option, I will post my progress in a later post then.
Sunday, November 14, 2010
Making the 4 man endgame tables available to the engine
After finishing the KPKP end game table I thought it is time now to make them available to the engine. For that I wrote a endgame advisor class that is able to access the stored table information.
Whenever the engine encounters a position with 4 or less pieces it asks the advisor whether it has a known score for that position, and if the answer is yes, it takes its score as value for the position and terminates the search in that branch of the search tree.
To ask the advisor upfront is necessary because not all possible 4 man positions are available. So far I only generated the ones where each side has one piece left. All positions where one side has 2 pieces and the other side has none are not available yet.
Those positions are not particular interesting as in general they are easy to win. It does not seem to make a lot of sense to dedicate disk space or memory to a table like king and 2 queens vs lone king. However tables like king and 2 bishops or king, bishop and knight vs king might be interesting. Because they contain long sometimes hard to might mate sequences.
On the other hand those endgames are very rare in practice and probably the engine will never encounter one in an actual game.
So this concludes my work on the endgame knowledge. With the 3 and 4 man tables available my engine has now a cheap and very accurate endgame DRAW detection. It took quite some time and was an very interesting exercise to work with the tables.
I will not continue with 5 man tables. There are some very important ones, like king, rook and pawn vs. king and rook, but the time to generate the tables is too long and they require to much space. So I will not include them into the engine package anyway. Those positions my engine has to solve by calculating.
Whenever the engine encounters a position with 4 or less pieces it asks the advisor whether it has a known score for that position, and if the answer is yes, it takes its score as value for the position and terminates the search in that branch of the search tree.
To ask the advisor upfront is necessary because not all possible 4 man positions are available. So far I only generated the ones where each side has one piece left. All positions where one side has 2 pieces and the other side has none are not available yet.
Those positions are not particular interesting as in general they are easy to win. It does not seem to make a lot of sense to dedicate disk space or memory to a table like king and 2 queens vs lone king. However tables like king and 2 bishops or king, bishop and knight vs king might be interesting. Because they contain long sometimes hard to might mate sequences.
On the other hand those endgames are very rare in practice and probably the engine will never encounter one in an actual game.
So this concludes my work on the endgame knowledge. With the 3 and 4 man tables available my engine has now a cheap and very accurate endgame DRAW detection. It took quite some time and was an very interesting exercise to work with the tables.
I will not continue with 5 man tables. There are some very important ones, like king, rook and pawn vs. king and rook, but the time to generate the tables is too long and they require to much space. So I will not include them into the engine package anyway. Those positions my engine has to solve by calculating.
Sunday, November 7, 2010
Success with the KPKP endgame table
After fixing all known problems with the king queen vs king pawn table I regenerated also all the king and piece vs king pawn tables so they are at least consitent.
I now proceed to the king pawn vs king pawn table. This is in a way special compared to the king and piece tables as with two opposite pawns on the board they possibility of "en passent" arises. All previous combination of 4 pieces did not have that problem.
To demonstrate this look at the following board
With Black to move White will win in 17 moves, so the value of that position is Mated in 17. But if the last move of white was f2-f4 then black can play g4 x f3 and wins in 11 moves (Mate in 11).
Unfortunately the table base has no history information of played moves because it is generated backwards from Mate positions. A clean solution would be to evaluate this position twice, with and without en passent possibility, but then you have to store whether you captured "en passent" or not as in the next iteration of retro table analysis the move generator may in case of en passent may only generate a single move (f2-f4).
This is quite tricky to implement as the data model so far does not allow the storage of a en passent flag. So I decided to implement a little hack here.
Whenever the move generator generates a move that will allow en passent captures for the opponent next turn (pawn double step with end position next to the opponent pawn) this move is deleted from the list of available moves and not considered in the analysis.
The assumption behind this is that a move that allows the opponent to capture the pawn will never be the best move, it is at most as good as another move from the list (e.g. the single pawn step move). This in fact seems to work quite well. The generated table is consistent and as far as I can tell correct.
I now proceed to the king pawn vs king pawn table. This is in a way special compared to the king and piece tables as with two opposite pawns on the board they possibility of "en passent" arises. All previous combination of 4 pieces did not have that problem.
To demonstrate this look at the following board
With Black to move White will win in 17 moves, so the value of that position is Mated in 17. But if the last move of white was f2-f4 then black can play g4 x f3 and wins in 11 moves (Mate in 11).
Unfortunately the table base has no history information of played moves because it is generated backwards from Mate positions. A clean solution would be to evaluate this position twice, with and without en passent possibility, but then you have to store whether you captured "en passent" or not as in the next iteration of retro table analysis the move generator may in case of en passent may only generate a single move (f2-f4).
This is quite tricky to implement as the data model so far does not allow the storage of a en passent flag. So I decided to implement a little hack here.
Whenever the move generator generates a move that will allow en passent captures for the opponent next turn (pawn double step with end position next to the opponent pawn) this move is deleted from the list of available moves and not considered in the analysis.
The assumption behind this is that a move that allows the opponent to capture the pawn will never be the best move, it is at most as good as another move from the list (e.g. the single pawn step move). This in fact seems to work quite well. The generated table is consistent and as far as I can tell correct.
Thursday, October 28, 2010
Still fighting the KQKP table
I fixed most of the issues with the KQKP table but there are still errors in it.
I find them when I consider symmetry properties of the board. When you have a position and flip the board vertical you end up with a mirrored position that should have the exact same value. Whenever the position and the mirrored position values are different you know there is a bug somewhere. This way I eliminated most of the bugs. The last I found is caused by not properly handling under promotions.
Consider the following position
If white promotes the pawn to a queen it is mated next move, moving with the king is slightly better as White then is "Mated in 2". The best move however is e7-e8 N. Then black must move out of check and white gains an additional move. So this positions value is "Mated in 3" but the table shows "Mated in 2" because it does not consider the under promotion to a knight.
So this is the next thing to fix and then hopefully the KQKP is ready and I can finally progress to the KPKP table.
I find them when I consider symmetry properties of the board. When you have a position and flip the board vertical you end up with a mirrored position that should have the exact same value. Whenever the position and the mirrored position values are different you know there is a bug somewhere. This way I eliminated most of the bugs. The last I found is caused by not properly handling under promotions.
Consider the following position
If white promotes the pawn to a queen it is mated next move, moving with the king is slightly better as White then is "Mated in 2". The best move however is e7-e8 N. Then black must move out of check and white gains an additional move. So this positions value is "Mated in 3" but the table shows "Mated in 2" because it does not consider the under promotion to a knight.
A nice shot of the inconsistency of the table.
So this is the next thing to fix and then hopefully the KQKP is ready and I can finally progress to the KPKP table.
Saturday, October 23, 2010
Further work on the 4 man end game tables
The work on the KPKP table base is quite challenging, because one has to consider the pawn promotions and also decide how to handle en passent positions. While working on the table it showed that there are some inconsistencies in the KQKP and other tables as well that popped up when handling the promotions. So I have to verify the base tables before I continue to work on the KPKP table. I hope to fix those issues pretty soon.
Thursday, October 14, 2010
Chess endgame table base KRKB
The next on my list for endgame tables was the endgame of king and rook vs king and bishop. Theory says that games with rook vs bishop or knight are drawish as they contain mostly draws and a few easy to spot wins where the rook is able to capture the piece (e.g. by pinning it to the king).
The table proved the theory however there are a few positions where the side with the rook can force a win that is not that obvious. I find those positions and the paths to mate from them quite interesting. One example is the following board
From the first look this position seems to be a safe draw for black. White is not able to capture the bishop in the near future. But the final table shows that this position is a forced with for White in 29 moves. The only winning move is 1. Ke1. The bishop is captured in move 17. So it would require a rather deep calculation for an engine to see the win in that position.
The table proved the theory however there are a few positions where the side with the rook can force a win that is not that obvious. I find those positions and the paths to mate from them quite interesting. One example is the following board
From the first look this position seems to be a safe draw for black. White is not able to capture the bishop in the near future. But the final table shows that this position is a forced with for White in 29 moves. The only winning move is 1. Ke1. The bishop is captured in move 17. So it would require a rather deep calculation for an engine to see the win in that position.
Thursday, October 7, 2010
Chess endgame table base KQKR
When I continued my work on the 4 man endgame table bases I started to work on a rather interesting 4 man combination. It is the King and Queen vs King and Rook end game. It is interesting because it is not trivial. All previous tables were mostly trivial as they contain easy forced wins (King and Queen vs King) or contain mostly draws (King and Queen vs King and Queen).
Consider the following position
Black threatens check mate with ... Rh4#. With white to move white can prevent the mate and win. But the table base shows that it requires at least 35 moves to do so. With regards to the 50 moves rule this requires accurate play and here the table base is quite helpful.
The generation of the table took quite some time on my computer also because I use board symmetries when storing the data but so far not in the calculation of the table. So I consider all 33.554.432 positions (2 * 2^24) and this took several hours.
Consider the following position
Black threatens check mate with ... Rh4#. With white to move white can prevent the mate and win. But the table base shows that it requires at least 35 moves to do so. With regards to the 50 moves rule this requires accurate play and here the table base is quite helpful.
The generation of the table took quite some time on my computer also because I use board symmetries when storing the data but so far not in the calculation of the table. So I consider all 33.554.432 positions (2 * 2^24) and this took several hours.
Sunday, September 26, 2010
4 man table bases
After the creation of the interesting 3 man table bases I move on to the 4 man stuff. The principle is the same but unfortunately they grow very heavily in size compared to the 3 man tables. At the 1st look they are 64 times bigger because a additional piece with 64 possible squares is included. This means uncompressed takes such a table 30 MB, which is quite a lot if you consider the fact that there are a lot of possible 4 man games and all of them require that space.
So I have to deal with board symmetry properties to contain the space required by the tables. I start with the games without pawns. Here the symmetries are the biggest and I need those tables for the games with the pawns anyway.
I'm starting to think of a conversion method that involves core squares like A1, B1, C1, D1, B2, C2, D2, C3, D3 and D4. Only positions with the white king on a core square are processed. If the white king is not on a core square the board is rotated or flipped and rotated until the white king is on a core square. This should save about 80% of space.
When the conversion is working I will explain it in more detail in a later post.
So I have to deal with board symmetry properties to contain the space required by the tables. I start with the games without pawns. Here the symmetries are the biggest and I need those tables for the games with the pawns anyway.
I'm starting to think of a conversion method that involves core squares like A1, B1, C1, D1, B2, C2, D2, C3, D3 and D4. Only positions with the white king on a core square are processed. If the white king is not on a core square the board is rotated or flipped and rotated until the white king is on a core square. This should save about 80% of space.
When the conversion is working I will explain it in more detail in a later post.
Wednesday, September 1, 2010
Creating a KPK endgame table base
After creating the KQK and KRK table bases I go to the more difficult stuff, which is a table base that involves pawns. I create a KPK (King and Pawn vs King) table base. There are 2 reasons that make this more difficult
First I initialize the table with the knowledge from the KQK table base. So on every promotion square I put a queen and score all possible positions with the score of that position from the KQK table base.
Here I encountered the first trap. Usually it is best to promote to a queen but not always.
Promoting the pawn to a queen will draw. The only winning move is under promoting the pawn to a rook. So when initializing the table make sure you consider rook promotions too when they score better than queen promotions.
After initializing the table I very much follow the method of generating positions further away from the known ones until all linked positions are generated and the table is no longer improved. The remaining unlinked unknown ones are draws. I ended up with a good table where the longest distance to mate was a "Mate in 28". But after verifying the content I found out that some positions were incorrectly scored.
This position was scored "Mate in 6". In fact it is a "Mate in 5". The reason is that I traced positions back from positions were the pawn was promoted and if in the position above the pawn moves to b8 and promotes to a queen it will in fact require 6 moves to mate (incl. the pawn move). However the move Kf5 will already "Mate in 5". But when this position was scored the position with the king on f5 was yet unknown and therefore the "Mate in 6" score was awarded to that position.
I tried several table generation methods that work around that issue (like only initializing with Mated in 0 scores) but all failed. The generated tables were worse than the one I already had. I finally accepted that the first pass will generated positions with paths to mates that are not necessarily the shortest ones.
I then tried a second pass on the filled table were I adjust the scores. I start with the Mated in 1 positions and verify them whether they are truly Mated in 1, I then verify the Mate in 2 positions whether shorter Mates are possible and so on until the "Mate in 28" positions are verified. The algorithm did quite some adjustments, much more than I expected, but the adjusted table now seems to be correct (My table access code does not distinguish between the promotions, it scores all promotions with the best score from a promotion, but this is just cosmetics, the only important thing is the correct score of each position).
- There is no mate position with a King and Pawn vs King. So you cannot just use the plain creation method from KQK here. You must promote the pawn to a queen or a rook before you can mate the king.
- White pawns and black pawns move in different directions. In a KQK endgame it makes no difference when you have a queen on b7 and it is the turn from the one with the queen, whether this is a black or a white queen. The distance to mate will be the same for both sides. In a KPK endgame a white pawn on b7 is very much different from a black pawn on b7.
First I initialize the table with the knowledge from the KQK table base. So on every promotion square I put a queen and score all possible positions with the score of that position from the KQK table base.
Here I encountered the first trap. Usually it is best to promote to a queen but not always.
Promoting the pawn to a queen will draw. The only winning move is under promoting the pawn to a rook. So when initializing the table make sure you consider rook promotions too when they score better than queen promotions.
After initializing the table I very much follow the method of generating positions further away from the known ones until all linked positions are generated and the table is no longer improved. The remaining unlinked unknown ones are draws. I ended up with a good table where the longest distance to mate was a "Mate in 28". But after verifying the content I found out that some positions were incorrectly scored.
This position was scored "Mate in 6". In fact it is a "Mate in 5". The reason is that I traced positions back from positions were the pawn was promoted and if in the position above the pawn moves to b8 and promotes to a queen it will in fact require 6 moves to mate (incl. the pawn move). However the move Kf5 will already "Mate in 5". But when this position was scored the position with the king on f5 was yet unknown and therefore the "Mate in 6" score was awarded to that position.
I tried several table generation methods that work around that issue (like only initializing with Mated in 0 scores) but all failed. The generated tables were worse than the one I already had. I finally accepted that the first pass will generated positions with paths to mates that are not necessarily the shortest ones.
I then tried a second pass on the filled table were I adjust the scores. I start with the Mated in 1 positions and verify them whether they are truly Mated in 1, I then verify the Mate in 2 positions whether shorter Mates are possible and so on until the "Mate in 28" positions are verified. The algorithm did quite some adjustments, much more than I expected, but the adjusted table now seems to be correct (My table access code does not distinguish between the promotions, it scores all promotions with the best score from a promotion, but this is just cosmetics, the only important thing is the correct score of each position).
Monday, August 30, 2010
Endgame Tablebases
At the moment I take a bit of rest from working on the engine and play around with a different aspect of chess, the endgame.
My engine posses a bit of endgame knowledge, like
force the downside king to the edge
keep the upside king close to the downside king
occupy the key squares of your pawn with your own king
This is usually enough for the engine to determine a quick mating sequence through search, even if the mate is not within its search depth yet.
A slight enhancement for an engine would be the usage of a endgame database where it stores for a variety of positions its correct value, so if the engine encounters such a position it knows its value instantly without searching further. Obviously the number of possible positions growths very rapidly with the number of remaining pieces on the board. In a 3 piece endgame (2 kings and 1 additional piece) there are 2^18 possible positions per remaining piece type and side to move ( a good amount of it is illegal, but anyway a huge number).
If the remaining piece is a knight or a bishop the position is a draw (insufficient material), so the interesting combination are king and queen or rook or pawn vs king, with pawn being probably the most interesting as it is not as trivial to determine whether the position is a win or a draw as with rook or queen. But it is also more difficult as the pawn must promote first turning the board into a king and queen vs king endgame.
So I started with the creation of a database of a king and rook or queen vs king endgame. The algorithm works as follows.
Again, I don't expect the engine to play stronger with that knowledge, but I think it is fun to enable the engine to announce deep mates, like "Mate in 16". However I have not decided how to make that knowledge available to the engine, at the moment it is just written to a file in the file system.
My engine posses a bit of endgame knowledge, like
force the downside king to the edge
keep the upside king close to the downside king
occupy the key squares of your pawn with your own king
This is usually enough for the engine to determine a quick mating sequence through search, even if the mate is not within its search depth yet.
A slight enhancement for an engine would be the usage of a endgame database where it stores for a variety of positions its correct value, so if the engine encounters such a position it knows its value instantly without searching further. Obviously the number of possible positions growths very rapidly with the number of remaining pieces on the board. In a 3 piece endgame (2 kings and 1 additional piece) there are 2^18 possible positions per remaining piece type and side to move ( a good amount of it is illegal, but anyway a huge number).
If the remaining piece is a knight or a bishop the position is a draw (insufficient material), so the interesting combination are king and queen or rook or pawn vs king, with pawn being probably the most interesting as it is not as trivial to determine whether the position is a win or a draw as with rook or queen. But it is also more difficult as the pawn must promote first turning the board into a king and queen vs king endgame.
So I started with the creation of a database of a king and rook or queen vs king endgame. The algorithm works as follows.
- Create all positions, evaluate them and mark those where the downside is mated as "Mated"
- Look through all the positions marked as "Mate" and mark all those positions the upside can reach in 1 move as "Mate in 1"
- Now generate all positions again and the moves in that position (it is downsides turn). Simulate the moves and look at the resulting positions. If all positions found are marked as "Mate in 1" the actual position gets "Mated in 1" score.
- Now generate all positions again and generate the moves for the upside, simulate the move and if you encounter 1 position marked "Mated in 1" the actual position gets the score of "Mate in 2".
- Go back to 3. but now look for positions where the downside cannot avoid a "Mate in 2" position. This position becomes "Mated in 2".
- Alternate between upside and downside processing until you make no longer progress (finding at least one score of a previously unknown position). Then you're done.
Its score in the database was determined as
- when it is upsides move = Mate in 2 (1. Rc2 Ka1 2. Rc1#)
- when its downsides turn = Mated in 1 (1. ... Ka1 2. Rc1#)
- and if the rook was not a rook but a queen, then it is a "Mate in 1" (1. Qe1#) or a Draw (Stalemate)
Again, I don't expect the engine to play stronger with that knowledge, but I think it is fun to enable the engine to announce deep mates, like "Mate in 16". However I have not decided how to make that knowledge available to the engine, at the moment it is just written to a file in the file system.
Wednesday, August 25, 2010
Implementing Late Move Reductions
After the unpleasant fixing of the transposition table design flaw I thought it is time to move to something more interesting to actually maybe improve the engine a bit.
I thought that "Late Move Reductions" is worth giving a try.
In a normal Alpha Beta tree you have 3 types of nodes
PV-nodes = nodes that have a score that ends up being inside the alpha beta window. These nodes have all moves searched, and the value returned is exact, which may propagate up to the root.
All-nodes = nodes in which no move's score exceeded alpha. Every move at an All-Node is searched, and the score returned is an upper bound, the exact score might be less.
Cut-nodes = nodes in which a beta cutoff is performed. The score returned is a lower bound (might be greater) on the exact score of the node.
Statistics show that in Cut Nodes with reasonable move ordering the cut off happens very early, within the first 3 to 4 moves. In "All Nodes" you search every move just to find out no one can improve your situation. Move ordering in All Nodes has no effect so a lot of search time the engine spends in handling the All Nodes. Unfortunatly you don't know that you are searching an All Node until you are done.
Late Move Reduction (LMR) tries to save some of the time here. The idea is that a move that is probably not a Cut Node (you searched the first 4 moves and are still there) and not a PV Node (you searched the probably best 3-4 moves after move ordering and no move was good enough to improve the score you already secured) is most likely an All Node. So the node is searched with a reduced depth to verify that it is really an All Node. This is where the name Late Move Reduction comes from, you reduce the late moves in such a node. If this reduced search reveals that you're guess was wrong you do a research of the moves otherwise you saved a lot of nodes.
However you should not reduce all moves just because they are late in the list. You should not reduce moves that give check, moves that respond to check, captures, promotions ... everything that is interesting or you miss something important.
After implementing this the engine searched a lot deeper but was actually playing weaker than the one without LMR. So I added another restriction that in nodes below a PV node no reduction takes place, as a wrong score here might more likely propagate up to the root. This seemed to do the trick.
I played 10 games of the engine with LMR against the engine without it, and the engine with LMR scored 7:3. One loss of the LMR engine was due to a time control issue where it lost on time in a winning position, so the loss is not a result of LMR. I find this a rather convincing improvement of the engine.
Arena tournament
10 games played / Tournament is finished
Level: Tournament 40/10
The end of the tournament, the engine with LMR as black will Mate in 2
I thought that "Late Move Reductions" is worth giving a try.
In a normal Alpha Beta tree you have 3 types of nodes
PV-nodes = nodes that have a score that ends up being inside the alpha beta window. These nodes have all moves searched, and the value returned is exact, which may propagate up to the root.
All-nodes = nodes in which no move's score exceeded alpha. Every move at an All-Node is searched, and the score returned is an upper bound, the exact score might be less.
Cut-nodes = nodes in which a beta cutoff is performed. The score returned is a lower bound (might be greater) on the exact score of the node.
Statistics show that in Cut Nodes with reasonable move ordering the cut off happens very early, within the first 3 to 4 moves. In "All Nodes" you search every move just to find out no one can improve your situation. Move ordering in All Nodes has no effect so a lot of search time the engine spends in handling the All Nodes. Unfortunatly you don't know that you are searching an All Node until you are done.
Late Move Reduction (LMR) tries to save some of the time here. The idea is that a move that is probably not a Cut Node (you searched the first 4 moves and are still there) and not a PV Node (you searched the probably best 3-4 moves after move ordering and no move was good enough to improve the score you already secured) is most likely an All Node. So the node is searched with a reduced depth to verify that it is really an All Node. This is where the name Late Move Reduction comes from, you reduce the late moves in such a node. If this reduced search reveals that you're guess was wrong you do a research of the moves otherwise you saved a lot of nodes.
However you should not reduce all moves just because they are late in the list. You should not reduce moves that give check, moves that respond to check, captures, promotions ... everything that is interesting or you miss something important.
After implementing this the engine searched a lot deeper but was actually playing weaker than the one without LMR. So I added another restriction that in nodes below a PV node no reduction takes place, as a wrong score here might more likely propagate up to the root. This seemed to do the trick.
I played 10 games of the engine with LMR against the engine without it, and the engine with LMR scored 7:3. One loss of the LMR engine was due to a time control issue where it lost on time in a winning position, so the loss is not a result of LMR. I find this a rather convincing improvement of the engine.
Arena tournament
| Rank | Engine | Score | En | En | S-B |
|---|---|---|---|---|---|
| 1 | Engine12 | 7,0/10 | · ·· ·· ·· ·· | 11===01=11 | 21,00 |
| 2 | Engine11 | 3,0/10 | 00===10=00 | · ·· ·· ·· ·· | 21,00 |
10 games played / Tournament is finished
Level: Tournament 40/10
The end of the tournament, the engine with LMR as black will Mate in 2
8/1p3kp1/3P3p/p1p1B3/P7/RP3qP1/5r2/3R2K1 w - - 0 40
Monday, August 23, 2010
Struggeling with a design flaw
When I was creating my engine I had to decide where to place the transposition tables. I decided to make them part of the board class as I wanted the verify its correct implementation first with the move generator. Let the perft calculation use the transposition table and if not the same number of moves is generated as before you know there is an error with it (the table itself, the hash key generation or make/unmake move). So the transposition table became a property of the board class in order to be available for the perft method.
I then developed my engine and my GUI further and it seemed to work very nicely this way. But when I finally sized the transposition table to a serious size of a couple of million entries I realized that the memory consumption of the GUI went also up very much. The reason is that the code for the board class is used by both the GUI and the engine. The GUI uses board properties like which square holds which piece and the move generation methods to verify the user input but by using the same code it also allocates the size of the transposition table.
So my GUI was suddenly consuming several hundreds of MB RAM.
I first tried to work around that by conditional compiling the GUI and engine
#IFDEF ENGINE
TTSIZE = 2097152
#ELSE
TTSIZE = 100
#ENDIF
It worked somehow (not really good because I had to explicitly save the unit with the constants to force a recompile of it). But I was not really happy with that work around anyway. I rather fix problems at the root.
So I decided to remove the transposition table from the board class and put it in the engine class although this requires a lot of code to be changed. I will spend some unpleasant hours on fixing my design. I hope the engine will not run slower after that and I do not introduce many new bugs.
Lessons learnt: Don't mess up your code with something that seems easier at first sight if it involves implementing something in a place where it does not belong to.
I then developed my engine and my GUI further and it seemed to work very nicely this way. But when I finally sized the transposition table to a serious size of a couple of million entries I realized that the memory consumption of the GUI went also up very much. The reason is that the code for the board class is used by both the GUI and the engine. The GUI uses board properties like which square holds which piece and the move generation methods to verify the user input but by using the same code it also allocates the size of the transposition table.
So my GUI was suddenly consuming several hundreds of MB RAM.
I first tried to work around that by conditional compiling the GUI and engine
#IFDEF ENGINE
TTSIZE = 2097152
#ELSE
TTSIZE = 100
#ENDIF
It worked somehow (not really good because I had to explicitly save the unit with the constants to force a recompile of it). But I was not really happy with that work around anyway. I rather fix problems at the root.
So I decided to remove the transposition table from the board class and put it in the engine class although this requires a lot of code to be changed. I will spend some unpleasant hours on fixing my design. I hope the engine will not run slower after that and I do not introduce many new bugs.
Lessons learnt: Don't mess up your code with something that seems easier at first sight if it involves implementing something in a place where it does not belong to.
Wednesday, August 18, 2010
Does my engine need an opening book
When programming a chess engine having an opening book is a nice feature. In my opinion it addresses to aspects
The reason to program a chess engine after all is to test my ability to create one not to test my ability to copy code or rely on information in existing databases created by others.
So lets think about how to do it myself ...
- The search in the engine is deterministic, in the same position with the same amount of time, search will always respond with the same move. Having an opening book where the engine can chose between multiple good moves for a position introduces a bit of randomness. The engine will not always play the same game.
- The engine saves time when playing the first moves as it doesn't have to search for a move. Without an opening book the moves from the engine are also not stupid but it took time to search for them. Engines with an opening book have a slight advantage against engines without one.
The reason to program a chess engine after all is to test my ability to create one not to test my ability to copy code or rely on information in existing databases created by others.
So lets think about how to do it myself ...
Friday, August 13, 2010
[BUG] UCI protocol implementation error
Today I realized an error in my implementation of the UCI protocol. It's been there for ages and I didn't noticed because I implemented the bug in the GUI as well as in the engine so they both could communicate perfectly.
Today I plugged the engine into another GUI called Arena (available freely at http://www.playwitharena.com) and here it became obvious. The engine was not able to initialize a board position when it is not the start position.
211.172-->2: position fen 4k3/p1p3p1/1p5p/8/8/1P5P/P1P3P1/4K3 w - - 0 1
211.172-->2: go wtime 600000 btime 600000 winc 0 binc 0 movestogo 40
211.218<--2: Invalid position or FEN string !
The reason was simple. The UCI position command is followed by either the keyword 'startpos' or 'fen'. My engine just wasn't aware of the 'fen' keyword. If the GUI did not send 'startpos' the engine tried to read in the fen string and failed because 'fen' are no valid FEN characters. It responded with invalid position or FEN string.
So fixing the error was now simple, tell the engine to expect the fen keyword and start reading the actual fen input with substring 3 instead of 2. Tell the GUI to send the fen keyword before the actual FEN.
And all is well again...
Today I plugged the engine into another GUI called Arena (available freely at http://www.playwitharena.com) and here it became obvious. The engine was not able to initialize a board position when it is not the start position.
211.172-->2: position fen 4k3/p1p3p1/1p5p/8/8/1P5P/P1P3P1/4K3 w - - 0 1
211.172-->2: go wtime 600000 btime 600000 winc 0 binc 0 movestogo 40
211.218<--2: Invalid position or FEN string !
The reason was simple. The UCI position command is followed by either the keyword 'startpos' or 'fen'. My engine just wasn't aware of the 'fen' keyword. If the GUI did not send 'startpos' the engine tried to read in the fen string and failed because 'fen' are no valid FEN characters. It responded with invalid position or FEN string.
So fixing the error was now simple, tell the engine to expect the fen keyword and start reading the actual fen input with substring 3 instead of 2. Tell the GUI to send the fen keyword before the actual FEN.
And all is well again...
Thursday, August 12, 2010
[BUG] Silly bug in the board evaluation
At some point in time every chess engine must be able to evaluate a given board position. The easiest way to do that is to just score the material. But then the engine moves around rather silly so you try to evaluate a position a bit better.
One of the things I consider in evaluation is the existence of castling rights. Whenever a side has preserved the right to castle it get a small bonus for it (one for king side and one for queen side). This way the engine gives not easily away the rights to castle by making a king move. It also tries now to take away the castling rights from the opponent.
So far so good, but this alone is not enough as the engine will now not castle because this means losing the rights to castle (after castling the engine can't do it again) and the bonuses associated with the rights. To get around this I rewarded a bigger bonus if the engine has made a castling move outweighing the loss of the castling rights.
Engine can castle king side +10
Engine can castle queen side +10
Engine has castled + 60
So if the engine castles it gets a overall bonus of +40 (60-10-10). This actually seemed to work pretty well. until recently I discovered a problem with that approach.
Consider the following position. This is one of the positions that search might encounter as a leaf node.
This position can be reached via various combination of moves (transpositions). If in the sequence of moves black has castled king side the position is evaluated with the +40 bonus for black. If the sequence of moves just involves black moving seperately with the rook and king it gets a penalty of -20 (black has given away both castling rights).
So the very same position gets 2 different scores depending on the move history, which I consider a bug in this case. I will try to fix it by removing the bonus for castling and giving a bonus for the king when located at the castling target positions (a good piece-square value for the king).
Another possibility when 2 positions get different scores is the issue of position repetition. Then we might approach a draw by repetition so the position is worse for the one with an advantage if it repeats itself. But this I actually consider a feature and not a bug.
One of the things I consider in evaluation is the existence of castling rights. Whenever a side has preserved the right to castle it get a small bonus for it (one for king side and one for queen side). This way the engine gives not easily away the rights to castle by making a king move. It also tries now to take away the castling rights from the opponent.
So far so good, but this alone is not enough as the engine will now not castle because this means losing the rights to castle (after castling the engine can't do it again) and the bonuses associated with the rights. To get around this I rewarded a bigger bonus if the engine has made a castling move outweighing the loss of the castling rights.
Engine can castle king side +10
Engine can castle queen side +10
Engine has castled + 60
So if the engine castles it gets a overall bonus of +40 (60-10-10). This actually seemed to work pretty well. until recently I discovered a problem with that approach.
rnbq1r2/pppppk1p/5n1b/8/3P4/P7/1PP1PPPP/RNBQKB1R w KQ -
Consider the following position. This is one of the positions that search might encounter as a leaf node.
This position can be reached via various combination of moves (transpositions). If in the sequence of moves black has castled king side the position is evaluated with the +40 bonus for black. If the sequence of moves just involves black moving seperately with the rook and king it gets a penalty of -20 (black has given away both castling rights).
So the very same position gets 2 different scores depending on the move history, which I consider a bug in this case. I will try to fix it by removing the bonus for castling and giving a bonus for the king when located at the castling target positions (a good piece-square value for the king).
Another possibility when 2 positions get different scores is the issue of position repetition. Then we might approach a draw by repetition so the position is worse for the one with an advantage if it repeats itself. But this I actually consider a feature and not a bug.
Wednesday, August 11, 2010
Coupling the Engine with the GUI - Part 2
In part 1 I described the engine interface on the GUI side. This is simpler as the GUI starts the engine as process and therefore has a handle to it, knows its process id and so on.
Programming the interface on the engine side is more difficult. The engine is started as a process and all it knows is, that it reads input from Standard In and writes output to Standard Out.
In Free Pascal you use the classes TIOStream for both purposes.
inputStream:=TIOStream.Create(iosInput);
outputStream:=TIOStream.Create(iosOutput);
Now letting the engine write some output to Standard Out is performed by a simple call. As the UCI protocol demands that lines end with a CRLF I wrapped a procedure around the output that appends #13#10 to the string and write to to the output stream.
procedure TEngine.writeOutput(anOutputStr : String);
begin
anOutputStr:=anOutputStr+chr(13)+chr(10);
outputStream.Write(anOutputStr[1],length(anOutputStr));
end;
Now to the really tricky part, Input reading from Standard In. There are several challenges
The UCI protocol demands that the engine is responsive even when calculating. In order to do that you have to poll for new input from time to time when doing a longer search for a best move. If you do that and no input is available the engine hangs and does not proceed with the search.
After trying and failing a lot I finally decided to run a different thread in my engine that does nothing than polling for new input. So it tries to read, blocks until something becomes available and if it receives input it sets a flag to let the engine know, something was received. All the engine does then is polling the flag from time to time.
The execution loop of the thread looks like this. (streamReader.Readln implements a blocking read from the input stream handling all the New Line variations)
while (not Terminated) do
begin
if newInputAvailable=False then
begin
S:=streamReader.Readln;
if S<>'' then
begin
newInput:=S;
newInputAvailable:=True;
end;
end;
end;
The tread implements also a read method the engine uses to retrieve the input. Whenever this method is called the tread knows it is safe to try to read again from the stream and maybe overwrite what he has read so far.
function TWatchStdIn.getNewInput:String;
begin
Result:='';
if newInputAvailable = False then Exit;
Result:=newInput;
newInputAvailable:=False;
newInput:='';
end;
This works very nicely but there is a problem with it. Using threads slows down the engine a lot. It is not the work the thread does, it is the pure existence of a thread. The performance is hit even if the thread is just declared and not even told to start executing. The reason is that the compiler builds a different program when he realizes that it runs more than one thread. Memory management within the program is more complex to make it thread safe and this costs performance.
To just outline how big the impact is I list the numbers for the perft calculation with threads and without it.
Depth Perft Time w/o Threads Time with Threads
5 4.865.609 1,265 sec 2,343 sec
6 119.060.324 29,687 sec 56,781 sec
So using threads almost doubles the time for the same work. For a chess engine this is a problem. Fortunately the impact seems much smaller when considering the complete search and evaluation process and as I see no real alternative to threads my engine is using them for the IO handling.
Programming the interface on the engine side is more difficult. The engine is started as a process and all it knows is, that it reads input from Standard In and writes output to Standard Out.
In Free Pascal you use the classes TIOStream for both purposes.
inputStream:=TIOStream.Create(iosInput);
outputStream:=TIOStream.Create(iosOutput);
Now letting the engine write some output to Standard Out is performed by a simple call. As the UCI protocol demands that lines end with a CRLF I wrapped a procedure around the output that appends #13#10 to the string and write to to the output stream.
procedure TEngine.writeOutput(anOutputStr : String);
begin
anOutputStr:=anOutputStr+chr(13)+chr(10);
outputStream.Write(anOutputStr[1],length(anOutputStr));
end;
Now to the really tricky part, Input reading from Standard In. There are several challenges
- You can't expect to receive the input line by line. All you receive is a bunch of bytes. You have to scan the received bytes for New Line characters which mark the end of one line and the start of another.
- You might receive input without any New Line characters at all. This happens when you try to read when the sending side was not yet finished sending. You can't just return that half completed line. You have to store it and complete it when new input becomes available.
- New Line characters are not always #13#10. The UCI protocol allows different combination for that, so you have to handle all possible New Line character variants.
- As far as I know there is no way to check for new input before you actually try to read it. Good old Pascal had this "keypressed" function, which returned true if the user pressed a key and you could use "readkey" after wards to actually read it. This does not exist anymore and actually Standard In is a stream, input might be available without any key pressed at all. The nasty thing with this is that reading from an empty stream blocks your execution until input becomes available.
The UCI protocol demands that the engine is responsive even when calculating. In order to do that you have to poll for new input from time to time when doing a longer search for a best move. If you do that and no input is available the engine hangs and does not proceed with the search.
After trying and failing a lot I finally decided to run a different thread in my engine that does nothing than polling for new input. So it tries to read, blocks until something becomes available and if it receives input it sets a flag to let the engine know, something was received. All the engine does then is polling the flag from time to time.
The execution loop of the thread looks like this. (streamReader.Readln implements a blocking read from the input stream handling all the New Line variations)
while (not Terminated) do
begin
if newInputAvailable=False then
begin
S:=streamReader.Readln;
if S<>'' then
begin
newInput:=S;
newInputAvailable:=True;
end;
end;
end;
The tread implements also a read method the engine uses to retrieve the input. Whenever this method is called the tread knows it is safe to try to read again from the stream and maybe overwrite what he has read so far.
function TWatchStdIn.getNewInput:String;
begin
Result:='';
if newInputAvailable = False then Exit;
Result:=newInput;
newInputAvailable:=False;
newInput:='';
end;
This works very nicely but there is a problem with it. Using threads slows down the engine a lot. It is not the work the thread does, it is the pure existence of a thread. The performance is hit even if the thread is just declared and not even told to start executing. The reason is that the compiler builds a different program when he realizes that it runs more than one thread. Memory management within the program is more complex to make it thread safe and this costs performance.
To just outline how big the impact is I list the numbers for the perft calculation with threads and without it.
Depth Perft Time w/o Threads Time with Threads
5 4.865.609 1,265 sec 2,343 sec
6 119.060.324 29,687 sec 56,781 sec
So using threads almost doubles the time for the same work. For a chess engine this is a problem. Fortunately the impact seems much smaller when considering the complete search and evaluation process and as I see no real alternative to threads my engine is using them for the IO handling.
Tuesday, August 10, 2010
Coupling the GUI with the Engine - Part 1
In my new engine programming approach I separated the GUI from the engine into two standalone executables. So now I have to find a way that they communicate with each other. The UCI (Universal Chess Interface) refers to the usage of Standard In and Standard Out of a process. So it was clear what to do, remains only the question how to do that in Free Pascal.
From the GUI perspective the engine is a process. Free Pascal defines a class TProcess, where you can specify something like the command line to the executable, what pipes are used and so on. When the GUI lanches it calles TProcess.Execute which starts the engine. It is running as process in the background. You see no engine window but it is listed in the Windows Task Manager process list.
To send something to the engine you add a CRLF (#13#10) to the string (defined in the UCI protocol) and call engine.Input.Write
To look for input and receive it from the engine you use
if Process.Output.NumBytesAvailable>0 then ReadCnt := Process.Output.Read(ReadBuf[Length(ReadBuf) - BUF_INC + 1], BUF_INC) else ReadCnt:=0;
Process.Output.NumBytesAvailable is very useful because it allows you to check whether there is any input at all and if not just return. In pipe communication trying to read from a pipe that is empty might block you execution until input becomes available in the pipe.
On the engine side of the communication Process.Output.NumBytesAvailable does not exist and this makes the interface on the engine side much more difficult and brings some nasty consequences.
More to that in another post
From the GUI perspective the engine is a process. Free Pascal defines a class TProcess, where you can specify something like the command line to the executable, what pipes are used and so on. When the GUI lanches it calles TProcess.Execute which starts the engine. It is running as process in the background. You see no engine window but it is listed in the Windows Task Manager process list.
To send something to the engine you add a CRLF (#13#10) to the string (defined in the UCI protocol) and call engine.Input.Write
ngCmd:=aCommand+chr(13)+chr(10);
procEngine.Input.Write(ngCmd[1], length(ngCmd));
procEngine.Input.Write(ngCmd[1], length(ngCmd));
To look for input and receive it from the engine you use
if Process.Output.NumBytesAvailable>0 then ReadCnt := Process.Output.Read(ReadBuf[Length(ReadBuf) - BUF_INC + 1], BUF_INC) else ReadCnt:=0;
Process.Output.NumBytesAvailable is very useful because it allows you to check whether there is any input at all and if not just return. In pipe communication trying to read from a pipe that is empty might block you execution until input becomes available in the pipe.
On the engine side of the communication Process.Output.NumBytesAvailable does not exist and this makes the interface on the engine side much more difficult and brings some nasty consequences.
More to that in another post
Saturday, August 7, 2010
Bit Twiddling Fundamentals - Finding the least significant bit in a BitBoard
As explained in the post about board representation BitBoards are very efficient for applying certain conditions onto the board. The result is a BitBoard where those bits are set for which all applied conditions are true.
In the example for the move generation of white pawns we advanced all pawns one rank and filtered out those pawns reaching the 8th rank and those hitting another piece. The result was a BitBoard with valid target squares for simple pawn moves.
In order to make use of that result we must now translate the set bit positions back into squares. The naive way is just looping through the bitboard and looking at each single bit whether it is 1.
Something like
This finds the least significant bit in bb. You can now do something with this information. Then you delete this bit in bb via bb := bb and NOT (2^pos) and start over again to find the next bit until bb is 0. Then all bits are processed.
This works but is slow. As finding a bit in a BitBoard is called millions of times during search for a best move you want that operation to be very fast. So this is not a reasonable approach.
There are better ways to do that. They might involve a look up tables or magic constants (search for DeBruijn).
The approach I took finally was relying on a processor instruction to do that. That makes the code less portable but it is most likely the fastest way to do that. Free Pascal supports in line assembler and my function looks like this
function getLSB(const Input: Int64): Byte; Assembler;
// Returns the least significant bit of a 64 bits number
// or ERROR if no bit is set
asm
bsf eax, dword ptr Input
jz @@0
jnz @@2
@@0:
bsf eax, dword ptr Input + 04h
jz @@1
add eax, 32
jnz @@2
@@1:
mov eax, ERROR
@@2:
end;
You must process the input in 2 steps as bsf (bit scan forward) works on 32 bit arguments.
I have similar functions for finding the most significant bit or counting the number of set bits in a BitBoard.
In the example for the move generation of white pawns we advanced all pawns one rank and filtered out those pawns reaching the 8th rank and those hitting another piece. The result was a BitBoard with valid target squares for simple pawn moves.
In order to make use of that result we must now translate the set bit positions back into squares. The naive way is just looping through the bitboard and looking at each single bit whether it is 1.
Something like
bb : BitBoard;
i : integer;
pos:=0;
while (pos<=63) and ((bb AND (2^pos))<>0) do inc(pos);
if pos<64 then ...
This finds the least significant bit in bb. You can now do something with this information. Then you delete this bit in bb via bb := bb and NOT (2^pos) and start over again to find the next bit until bb is 0. Then all bits are processed.
This works but is slow. As finding a bit in a BitBoard is called millions of times during search for a best move you want that operation to be very fast. So this is not a reasonable approach.
There are better ways to do that. They might involve a look up tables or magic constants (search for DeBruijn).
The approach I took finally was relying on a processor instruction to do that. That makes the code less portable but it is most likely the fastest way to do that. Free Pascal supports in line assembler and my function looks like this
function getLSB(const Input: Int64): Byte; Assembler;
// Returns the least significant bit of a 64 bits number
// or ERROR if no bit is set
asm
bsf eax, dword ptr Input
jz @@0
jnz @@2
@@0:
bsf eax, dword ptr Input + 04h
jz @@1
add eax, 32
jnz @@2
@@1:
mov eax, ERROR
@@2:
end;
You must process the input in 2 steps as bsf (bit scan forward) works on 32 bit arguments.
I have similar functions for finding the most significant bit or counting the number of set bits in a BitBoard.
Friday, August 6, 2010
New board representation
I learnt with my first approach with a chess engine the way how you store the chess board is an important (if not the most important) decision when you start programming. The way you store the content of the board determines how efficient can you generate moves or evaluate the current situation of the board. When finding a move the engine generates hundreds of thousands of moves and evaluates millions of positions so you want to do that very efficiently.
In my first approach I used a 12x12 board with two rings of invalid squares around the actual board. The advantage of this approach is that you know instantly for any given square whether it is empty or what type of piece it holds. I also stored the positions of both kings. So if you want to know whether one side is in check you don't have to loop over all the squares just to find out where the kings are.
But even with this information at hand generating moves is very slow. You have an outer loop that loops over all squares, if it hits a piece of the side to move it jumps to piece specific code for generating the moves for that piece. For sliding pieces like bishop, rook or queen this involves inner loops that travel along the lines until they hit a piece or invalid square (the edge of the board).
If you research a bit how other engines represent the board you find a method called BitBoards for storing the board information. This is actually a very clever way to do that but you should be comfortable with Boolean algebra (bitwise AND, OR, NOT and XOR).
The main idea is that you store for every piece type a 64 bit Integer in which a 1 bit on a certain position in that integer stands for a piece of that type on that square. So you will need in total 12 of that Int64 for all types of pieces (6 for white and 6 for black). It makes also sense to have some helper BitBoards like OccupiedSquares, EmptySquares, WhitePieces and BlackPieces. It is possible to generate them any time by bitwise OR of the piece BitBoards but as they are required very often it is faster to maintain them when executing moves.
To give a glimpse what BitBoards can do here the method for generating standard white pawn moves.
The pawn positions on the board are in a BitBoard called w_Pawns. In the bitboard bit 0 stands for square A1, bit 1 for B1 and bit 63 for square H8. To generate the moves we do the following
// piece as arguments
We have now generated all simple pawn moves in one go. Very efficient. How to efficiently determine the position of a 1 bit in a bitboard is explained in a later post.
Although BitBoards are sufficient to know what piece is located on what square, it requires some effort to answer the question what piece stands on a certain square. I have to loop through all the piece BitBoards until I find the one with the 1 bit for that square set. So I decided to have in addition to BitBoards a traditional array where I maintain the content of each square.
So for whatever information I need, I either look at the BitBoards or the square array. Of course there is an overhead in move execution as both data structures must be maintained, but I decided it is worth it.
In my first approach I used a 12x12 board with two rings of invalid squares around the actual board. The advantage of this approach is that you know instantly for any given square whether it is empty or what type of piece it holds. I also stored the positions of both kings. So if you want to know whether one side is in check you don't have to loop over all the squares just to find out where the kings are.
But even with this information at hand generating moves is very slow. You have an outer loop that loops over all squares, if it hits a piece of the side to move it jumps to piece specific code for generating the moves for that piece. For sliding pieces like bishop, rook or queen this involves inner loops that travel along the lines until they hit a piece or invalid square (the edge of the board).
If you research a bit how other engines represent the board you find a method called BitBoards for storing the board information. This is actually a very clever way to do that but you should be comfortable with Boolean algebra (bitwise AND, OR, NOT and XOR).
The main idea is that you store for every piece type a 64 bit Integer in which a 1 bit on a certain position in that integer stands for a piece of that type on that square. So you will need in total 12 of that Int64 for all types of pieces (6 for white and 6 for black). It makes also sense to have some helper BitBoards like OccupiedSquares, EmptySquares, WhitePieces and BlackPieces. It is possible to generate them any time by bitwise OR of the piece BitBoards but as they are required very often it is faster to maintain them when executing moves.
To give a glimpse what BitBoards can do here the method for generating standard white pawn moves.
The pawn positions on the board are in a BitBoard called w_Pawns. In the bitboard bit 0 stands for square A1, bit 1 for B1 and bit 63 for square H8. To generate the moves we do the following
// we generate the target squares by shifting all pawns 8 bits left and remove those
// who hit another piece or reach the 8th rank (those are special as they promote
// and handled differently)
// BB_RANKS is a array of BitBoard constants, that have bits set that specify
// a certain rank e.g. BB_RANKS[8] is set to $FF00000000000000
// TMove.Create accepts start square, target square, moved piece and captured// piece as arguments
targetSq_bb := (w_Pawns shl 8) AND EmptySquares AND NOT(BB_RANKS[8]);
for each bit=1 in targetSq_bb do
targetSq := bitPosition;
move := TMove.Create(targetSq-8, targetSq, W_Pawn, NONE);
next
We have now generated all simple pawn moves in one go. Very efficient. How to efficiently determine the position of a 1 bit in a bitboard is explained in a later post.
Although BitBoards are sufficient to know what piece is located on what square, it requires some effort to answer the question what piece stands on a certain square. I have to loop through all the piece BitBoards until I find the one with the 1 bit for that square set. So I decided to have in addition to BitBoards a traditional array where I maintain the content of each square.
So for whatever information I need, I either look at the BitBoards or the square array. Of course there is an overhead in move execution as both data structures must be maintained, but I decided it is worth it.
Thursday, August 5, 2010
Getting started
I'm starting this blog to document the steps for creating my own engine. I kicked off this project in December 2009 and dedicate since then a part of my spare time to it. I always liked programming and as a student I created Checkers and Othello engines just for fun. Chess I considered to difficult in regards of the ability of hardware back then and my favor for more complex programming languages like Pascal or C instead of Assembler.
Now hardware is much more powerful and I guessed probably powerful enough to allow me to create an engine that plays a decent game of chess. So I started this project. I decided to use Free Pascal for it. Most of the engines out there are written in C or C++ but I wanted I nice little GUI too. For that I always liked Delphi but I only have a 16 bit version of it available (Delphi 1.0) which is not suitable for that purpose and I didn't want to invest into a current version for my fun project either, so I took Free Pascal (Lazarus).
The first version of my engine was no engine at all. It was a GUI able to play chess. It did not use any protocol as I was not aware that something like chess protocols exist.
It used an array structure of 12x12 as board representation (12x12 not 8x8 as I thought it might be easier to implement an "off the board" detection when I place 2 rings of invalid squares around the 8x8 board and do not generate a move when the target square is a invalid square). Moves where generated by looping through all the pieces and jumping, moving or sliding them until they hit a piece or invalid square. It worked by it was awfully slow.
To generate the 119.060.324 nodes that are 6 half moves (plys) deep from the initial position it took 96 sec. For search it used a plain Alpha-Beta Mini-Max algorithm with a short quiescence search (stops after 4 plys). This version was able to calculate 4-5 plys deep to get a move in a reasonable amount of time, which is enough to play not a totally stupid game of chess but not good enough to satisfy me.
I decided to start the project all over again and doing some research first. I decided to use only some of the old user interface code for the new GUI and create a real engine as standalone executable using those things I leaned while doing my chess engine programming research.
Now hardware is much more powerful and I guessed probably powerful enough to allow me to create an engine that plays a decent game of chess. So I started this project. I decided to use Free Pascal for it. Most of the engines out there are written in C or C++ but I wanted I nice little GUI too. For that I always liked Delphi but I only have a 16 bit version of it available (Delphi 1.0) which is not suitable for that purpose and I didn't want to invest into a current version for my fun project either, so I took Free Pascal (Lazarus).
The first version of my engine was no engine at all. It was a GUI able to play chess. It did not use any protocol as I was not aware that something like chess protocols exist.
It used an array structure of 12x12 as board representation (12x12 not 8x8 as I thought it might be easier to implement an "off the board" detection when I place 2 rings of invalid squares around the 8x8 board and do not generate a move when the target square is a invalid square). Moves where generated by looping through all the pieces and jumping, moving or sliding them until they hit a piece or invalid square. It worked by it was awfully slow.
To generate the 119.060.324 nodes that are 6 half moves (plys) deep from the initial position it took 96 sec. For search it used a plain Alpha-Beta Mini-Max algorithm with a short quiescence search (stops after 4 plys). This version was able to calculate 4-5 plys deep to get a move in a reasonable amount of time, which is enough to play not a totally stupid game of chess but not good enough to satisfy me.
I decided to start the project all over again and doing some research first. I decided to use only some of the old user interface code for the new GUI and create a real engine as standalone executable using those things I leaned while doing my chess engine programming research.
Subscribe to:
Comments (Atom)